Some exploratory data analysis on the dataset.
The power variable represents wind turbine power output and the speed values are wind speed values. This is all that has been provided. There are no null values in the dataset but there are 49 observations with zero values.
While there is only one zero value for the speed variable, there are 49 zero values for the power variable.
Some research below suggests that the wind speed values are measured in metres per second and that the power values are measured in kilowatts, although it could be megawatts based on the values in the dataset. However this will not affect the analysis.
Exploratory data analysis generally involves both non-graphical methods which include calculation of summary statistics and graphical methods which summarises the data in a picture or a plot. Visualisations can highlight any obvious relationships between the different variables in the dataset and to identify any groups of observations that are clearly separate to other groups of observations.
df.head()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
df.tail()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
# have a look at the dataset
df.sort_values(by='power', ascending=False).head()
df.sort_values(by='power').head()
df.sort_values(by='speed').head()
# check for null values
df.isnull().values.any()
df.isnull().sum()
# check for zero values
df.isin([0]).sum()
speed 1
power 49
dtype: int64
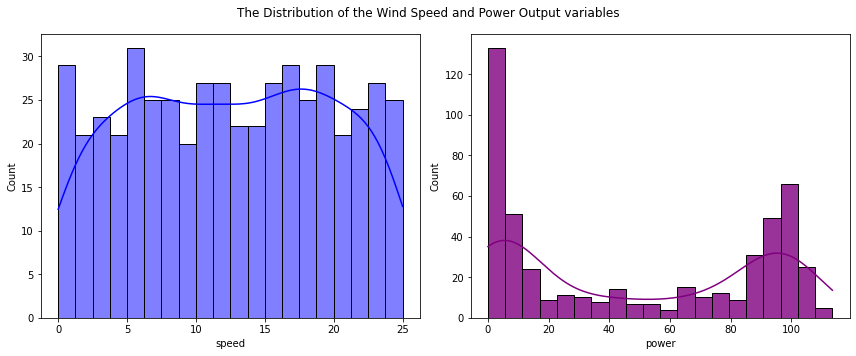
Looking at the distribution of the data
A histogram can be used to show the distribution of a single quantitative variable such as speed or power values, including the centre and spread of the distribution and if there is any skew in the data. Wind speed appears to be uniformly distributed with values spread out from zero up to a maximum value of 25. Power output values on the other hand looks to be bimodal with two defined peaks, one around zero power values and the second around the 100 kilowatt mark. The first peak is betweeen power values of 0 and 5. This is not surprising given the large number of zero power values in this dataset. Almost 10% of the power values supplied are zero. There is another smaller peak around values of 95-100. Most of the remaining power values fall between 18 and 85.
%matplotlib inline
# plot the histograms of Speed values
f, axs = plt.subplots(1, 2, figsize=(12, 5))
sns.histplot(data=df, x="speed", ax=axs[0], bins=20, kde=True,color="blue")
sns.histplot(data=df, x="power", alpha=.8, legend=False, ax=axs[1], bins=20, kde=True, color="purple")
#plt.title("Speed vs Power");
plt.suptitle("The Distribution of the Wind Speed and Power Output variables")
plt.savefig("images/The Distribution of the Wind Speed and Power output variables.png")
f.tight_layout()
The relationship between the Wind Speed and Power Output variables:
# create the plot
plt.style.use('ggplot')
# Plot size.
plt.rcParams['figure.figsize'] = (14, 8)
plt.scatter(df['speed'],df['power'], marker=".")
# https://stackoverflow.com/questions/12608788/changing-the-tick-frequency-on-x-or-y-axis-in-matplotlib
plt.yticks(np.arange(min(df['power']), max(df['power'])+1, 5.0))
plt.xticks(np.arange(min(df['speed']), max(df['speed'])+1, 2.0))
#sns.scatterplot(x=df['speed'],y=df['power'], marker="x")
plt.grid(True)
plt.xlabel("Wind speed (m/s)")
plt.ylabel("Power (kilowatts)")
# add title
plt.title("Wind Speed vs Power Output", fontsize=20);
plt.savefig("images/Wind Speed Power scatterplot.png")
plt.show()
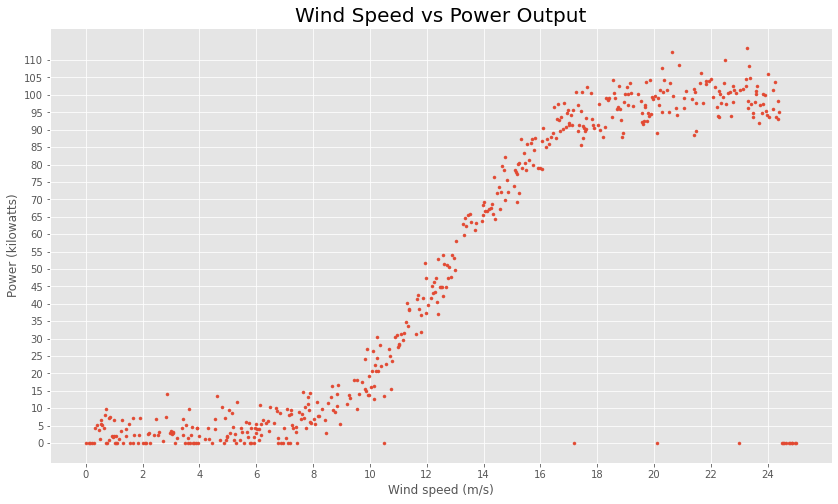
Scatter plots are useful to identify trends and patterns in a dataset which might indicate a relationship between two numerical variables such as we have in this dataset. The ordered pairs of numbers consisting of the independent variable wind ‘speed’ and the dependent variable ‘power’ output are plotted below resulting in a joint distribution of the two variables. Each point represents an actual observation is the dataset with a speed and a corresponding power value. The scatter plot above shows an increasing linear trend in the middle range of the wind speed values. This would indicate that for increasing wind speeds in this range, power output values do increase, but only after a minimum wind speed has been reached. Power outputs then increase in line with increases in wind speed until it reaches a peak and levels off. The plot suggests that very low winds may not be enough to get the turbine going and that the turbines have a maximum power level. Once the turbine is in motion perhaps little is required to keep it going. Some of the power generated might be consumed by the turbine itself at low levels to get it started.
Correlation and Covariance of Wind Speed and Power Output values:
For two quantitative variables such as the wind speed and power values, the covariance and correlation can also be used to determine whether a linear relationship between variables does exist and to show if one variable tends to occur with large or small values of another variable. The correlation statistics puts a numerical value on the strength and direction of the relationship. The correlation coefficient here of 0.85 shows there is a very strong positive relationship between the wind speed and turbine power output. The scatter plot shows a curved relationship between the variables. There appears to be a curvilinear pattern in the data.
df.corr()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
Some summary statistics of the dataset:
When looking at quantitative variables such as wind speed and power values, the characteristics of interest are the centre, spread, modality, the shape of the distribution and the outliers. The central tendency or location of the data distribution is determined by the typical or middle values. While the mean value is the average value in the dataset it may not be typical of the values in the dataset if there are very small or very large values in the dataset. The median is another measure of central tendancy - it is the middle value after all the values are put in an ordered list. The mean and median are similar for symmetric distributions whereas for unimodal skewed distributions the mean will be more in the direction of the long tail of the distribution. The median can be considered a more typical value in the dataset or closer to some of the typical values and is also considered robust which means that removing some of the data will not tend to change the value of the median. A few extreme values will not affect the median as they would affect the mean. In this dataset the mean and median wind speed values are similar at approx 12.5 to 12.6 metres per second. The median power value is just over 41 unit compared to the mean power value of 48 (kws). As we saw above, there are many zero values for power in the dataset. At least 10% of the power values in the dataset are zero.
The variance and standard deviation statistics can be used to show the spread of the distribution of the speed and power data values and how far away from the centre the data points are located. The variance is the average of the squared deviations of each observation from the centre or mean of the data while the standard deviation is the square root of the variance and is in the same units as the data and therefore can be more easily interpreted. The range of values in the data is shown by the minimum and maximum values and is not considered a robust measure of spread but it is useful for showing possible errors or outliers.
The percentiles or quartiles of the speed and power values can be used to see the spread of the data values. The Interquartile range (IQR) is calculated by taking the 75% percentile or 3rd quartile minus the 25% percentile or first quartile and captures half of the values, the middle values of the data. Data that is more spread out will have a higher IQR. The IQR is considered a more robust measure of spread than the variance and standard deviation and will be more clearly shown in the boxplots further down. The IQR does not consider the data below the 25% percentile or above the 75% percentile which may contain outliers. The statistics here show that the power output variable in this dataset is much more spread out or variable than the wind speed variable.
# using pandas summary statistics of the numerical values
df.describe()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
print("The mean speed value is %.3f" %df['speed'].mean(),"while the median speed value is %.3f" %df['speed'].quantile(q=0.5))
print("The mean power value is %.3f" %df['power'].mean(),"while the median power value is %.3f" %df['power'].quantile(q=0.5))
#print(f"The variance and standard deviations of speed values are {df['speed'].var():.3f} and {df['speed'].std():.3f}")
#print(f"The variance and standard deviations of power values are {df['power'].var():.3f} and {df['power'].std():.3f}")
print(f"The standard deviations of speed values is {df['speed'].std():.3f}")
print(f"The standard deviations of power values is {df['power'].std():.3f}")
print(f"The minimum speed value is {df['speed'].min()} while the maximum speed value is { df['speed'].max()} giving range of {df['speed'].max() - df['speed'].min()}")
print(f"The minimum Power value is {df['power'].min()} while the maximum power value is { df['power'].max()} giving range of {df['power'].max() - df['power'].min()}")
print(f"The median speed value is {df['speed'].quantile(q=0.5)} with the IQR ranging from {df['speed'].quantile(q=0.25):.2f} to {df['speed'].quantile(q=0.75):.2f}")
print(f"The median power value is {df['power'].quantile(q=0.5)} with the IQR ranging from {df['power'].quantile(q=0.25):.2f} to {df['power'].quantile(q=0.75):.2f}")
The mean speed value is 12.590 while the median speed value is 12.550
The mean power value is 48.015 while the median power value is 41.645
The standard deviations of speed values is 7.225
The standard deviations of power values is 41.615
The minimum speed value is 0.0 while the maximum speed value is 25.0 giving range of 25.0
The minimum Power value is 0.0 while the maximum power value is 113.556 giving range of 113.556
The median speed value is 12.5505 with the IQR ranging from 6.32 to 18.78
The median power value is 41.6455 with the IQR ranging from 5.29 to 93.54
f, axes = plt.subplots(1, 2, figsize=(12, 4))
sns.set(style="ticks", palette="pastel")
sns.boxplot(y=df['speed'], ax=axes[0], color="blue")
# add a title
axes[0].set_title("Boxplot of Wind Speed values")
sns.boxplot(y=df['power'], ax=axes[1], color="purple")
axes[1].set_title("Boxplot of Power Output Values");
plt.savefig("images/Boxplots of Wind Speed and Power Output values.png")
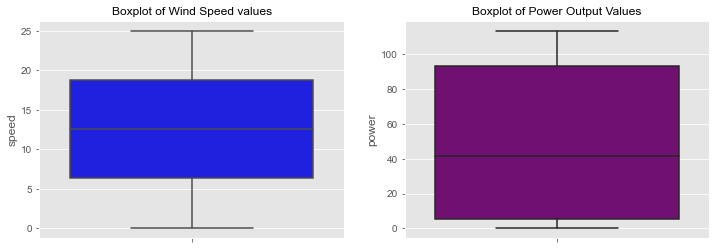
The skewness of the data is a measure of assymetry which can be seen by the lopsidedness of a boxplot. Wind speed appears to be quite symmetric. The wind speed boxplot is cut pretty much in half by the median. Power appears to be somewhat skewed to the right as the boxplot shows more of the box to the right or above the median line. A boxplot with the median closer to the lower quartile is considered positively skewed. Positively skewed data has the mean greater than the median and it can be interpreted as having a higher frequency of high valued scores. The lower values of power are closer together than the higher power values.
Regression plots:
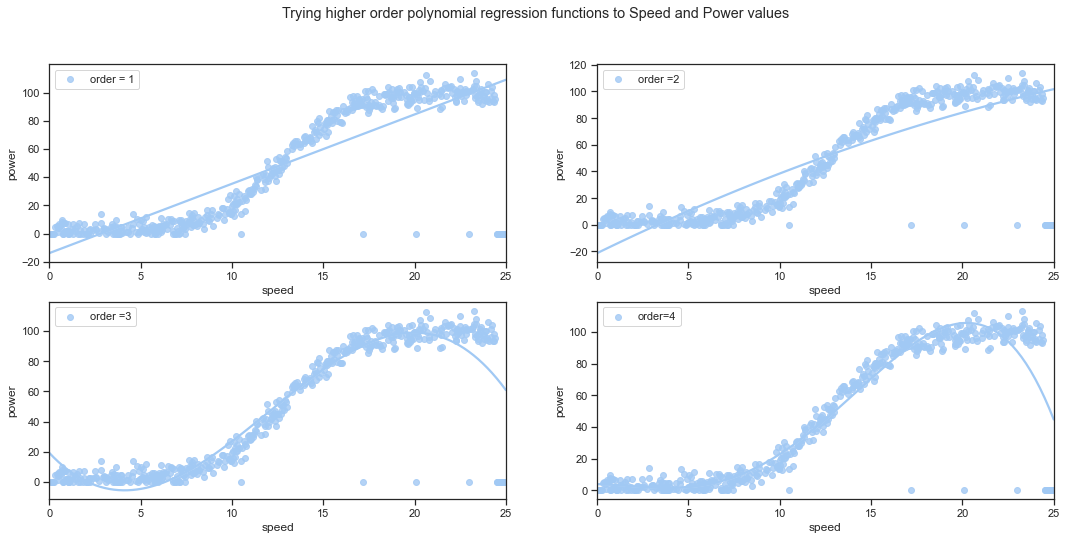
The Python Seaborn library has some regression plots that can be used to quickly visualise relationships and patterns that may exist in the data. They use statistical models to estimate a simple relationship between sets of observations and are mainly used to visualise patterns in a dataset during the exploratory data analysis. The scatter plot earlier showed a relationship between wind speeds and wind turbine power that is non-linear. There does seem to be a somewhat linear relationship for wind speeds between values of about 10 up to about 18 or so. The plot below shows that the polynomial with order 3 looks a much better fit to the line than the first or second order linear regression lines. It is important not to go down the road of overfitting the data though.
f, axes = plt.subplots(2, 2, figsize=(18, 8))
x = "speed"
y = "power"
sns.regplot(x="speed", y="power", data=df, ax=axes[0,0], label="order = 1", ci=False); axes[0,0].legend()
sns.regplot(x="speed", y="power", data=df, order=2, ax=axes[0,1], label="order =2", ci=False); axes[0,1].legend()
sns.regplot(x="speed", y="power", data=df, order=3, ax=axes[1,0], label="order =3", ci=False); axes[1,0].legend()
sns.regplot(x="speed", y="power", data=df, order=4, ax=axes[1,1], label = "order=4", ci=False); axes[1,1].legend()
plt.legend()
plt.suptitle("Trying higher order polynomial regression functions to Speed and Power values")
plt.savefig("images/Higher Order regression plots.png")
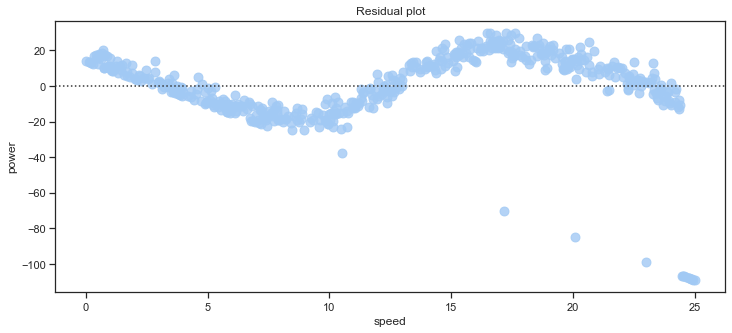
Residual plots can be used to check whether the simple regression model of speed ~ power is appropriate for a dataset. The seaborn residplot fits and removes a simple linear regression and then plots the residual values for each observation. Ideally, these values should be randomly scattered around y = 0. If there is structure in the residuals, this suggests that simple linear regression is not appropriate for the data. The residual plot here has a shape which suggest non-linearity in the data set as expected.
plt.rcParams['figure.figsize'] = (12, 5)
sns.residplot(x="speed", y="power", data=df, scatter_kws={"s": 80})
plt.title("Residual plot");
plt.savefig("images/Residual plot.png")